목차
- Dijkstra's algorithm (다익스트라 알고리즘)
- Example
- Oscillation problem (진동 문제)
1. Dijkstra’s algorithm
인접한 노드들 중 최적 경로인 노드를 계속 선택하여 최적 경로 Tree를 만드는 알고리즘
Link status algorithm은 Dijkstra’s algorithm을 기반으로 만들어짐
특징
- 모든 노드에 대한 비용을 알고 있을 때 사용 가능
- 각 라우터들이 link state broadcast 하기 때문에 사용 가능
- 모든 노드가 동일한 정보를 가짐
- 하나의 노드(source)에서 모든 노드로의 최소 비용 경로 계산
- 해당 노드에 대한 포워딩 테이블 주어짐
- 반복적인 작업을 수행한 후 최소 비용 경로를 파악
2. Example
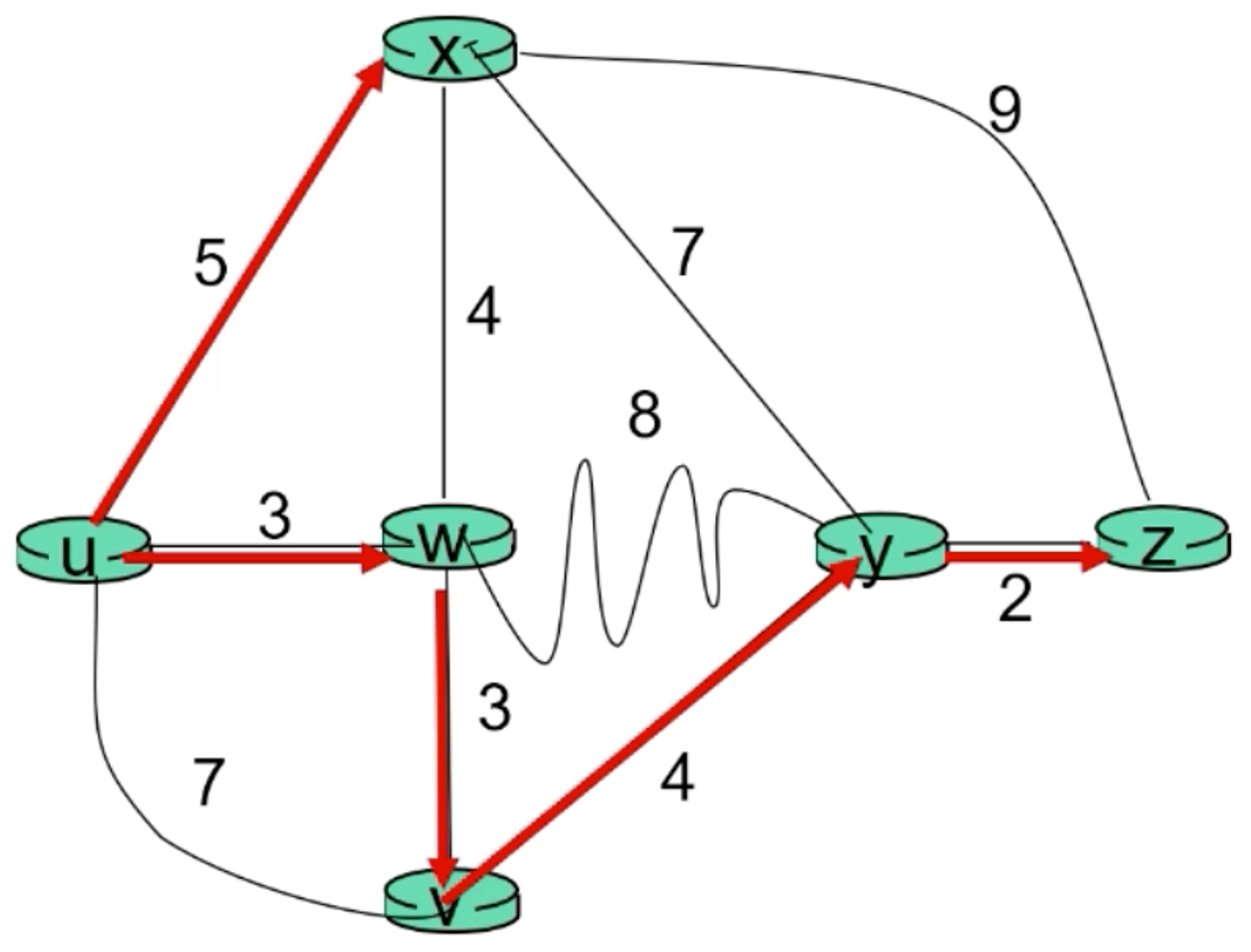

- c(x,y): 노드 x에서 y로 링크 비용; 직접 이웃이 아닌 경우 ∞
- D(v): 소스에서 대상까지의 경로 비용의 현재 값. v
- p(v): 소스에서 v로 가는 경로의 이전 노드
- N': 최소 비용 경로가 확실하게 알려진 노드 집합
각 step 마다 N과 인접한 노드의 최단경로를 계산
해당 노드들까지 가는 경로 중 가장 작은 값을 N에 포함
N’의 집합의 원소들이 그래프의 집합의 원소들과 같아지면 알고리즘 종료
Dijkstra’s algorithm 시간복잡도: O(n^2)
최적화 구현을 한다면 시간복잡도: O(n log n)
3. Oscillation problem
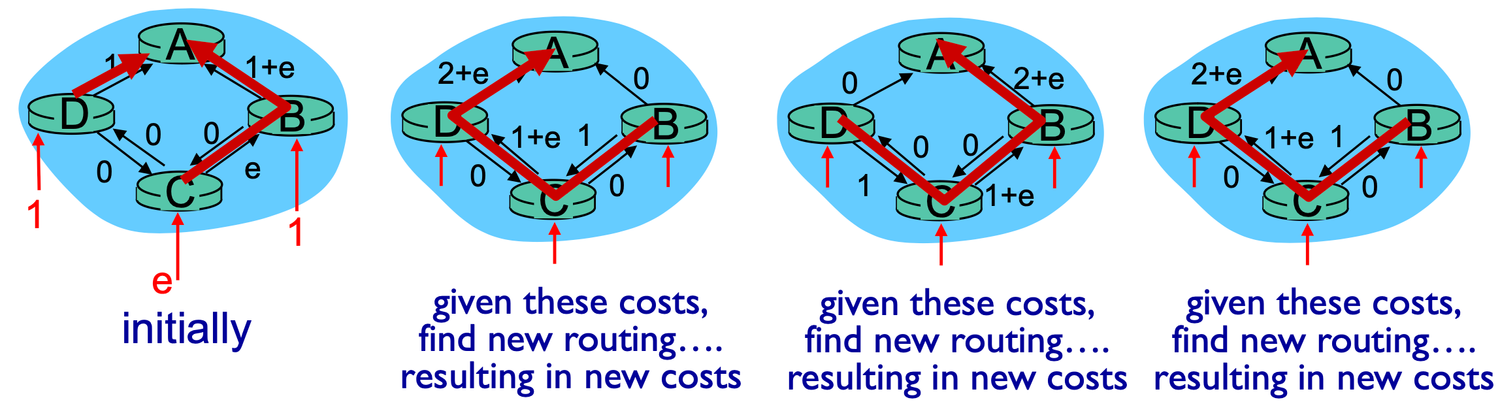
D, B에 단위가 1인 패킷이 도착하고 C에 단위가 e인 큰 패킷이 도착했다고 가정, 모든 목적지는 A
- C는 B를 경유해 단위가 e인 패킷을 A로 보내기로 결정
- C→B 경로의 cost=e
- B→A 경로의 cost=1+e
- B 입장에서 B→A의 cost=1+e, B→C→D→A의 cost=0+0+0+1=1이므로 패킷을 B→C→D→A의 경로로 보내기로 결정
- B→C 경로의 cost=1
- C→D 경로의 cost=1+e
- D→A 경로의 cost=2+e
- D 입장에서 D→A의 cost=2+e, D→C→B→A의 cost=0+0+0=0이므로 패킷을 D→C→B→A의 경로로 보내기로 결정
- D→C 경로의 cost=1
- C→B 경로의 cost=1+e
- B→A 경로의 cost=2+e
- 위와 같은 상황 반복
Oscillation(진동) 문제: Dijkstra’s algorithm 사용 시 위와 같은 상황이 반복되어 무한 루프에 빠지게 되는 문제
→ link status 알고리즘에서는 링크 상태 공유 시 랜덤 딜레이를 주어 동시에 경로를 바꾸는 것을 최대한 방지함
Link status algorithm vs. Distance vector algorithm
[네트워크] #18 라우팅 프로토콜, Link status algorithm vs. Distance vector algorithm
목차 라우팅 프로토콜 Link status algorithm vs. Distance vector algorithm 1. 라우팅 프로토콜 라우팅 프로토콜 목표: 라우터 네트워크를 통해 송신 호스트에서 수신 호스토로의 최적의 경로를 결정 네트워
campus-coder.tistory.com
'전공 > 네트워크' 카테고리의 다른 글
| [네트워크] #21 Intra-AS, Inter-AS routing (OSPF, BGP, Intra-AS vs. Inter-AS) (0) | 2023.12.06 |
|---|---|
| [네트워크] #20 Distance vector 알고리즘 (Bellman-Ford equation, Example, 문제점) (1) | 2023.12.06 |
| [네트워크] #18 라우팅 프로토콜, Link status algorithm vs. Distance vector algorithm (0) | 2023.12.06 |
| [네트워크] #17 IP (개념, Datagram 형식, IPv4, IPv6, 주소 접근, NAT) (2) | 2023.12.05 |
| [네트워크] #16 라우터 (구조, 기능, 포워딩, 스케줄링 정책) (2) | 2023.12.05 |