서론
2서클 과제인 push_swap에 대해 정리해보려 한다.
push_swap은 인자로 받은 숫자들을 두 개의 스택(stack_a, stack_b)을 이용해 최대한 적은 명령어를 사용하여 정렬하는 알고리즘을 구현하는 과제이다. 필자는 push_swap 평가를 처음 갔을 때 그리디 알고리즘을 사용하여 이 과제를 해결할 수 있다는 말을 듣고 매력적으로 느껴 그리디 알고리즘을 선택하게 되었다.
push_swap 그리디 알고리즘
그리디 알고리즘은 매 결정마다 그 순간 최적의 결정을 내리는 과정을 반복해 최종적인 해답에 도달하는 알고리즘이다. 제한된 명령어만 사용할 수 있는 push_swap에 어떻게 그리디 알고리즘을 적용시킬 수 있을까?
답은 정렬되어 있지 않은 stack_b의 원소를 정렬된 stack_a로 최소 개수의 명령어를 사용하여 옮기는 것이다.
정렬되어 있는 stack_a에 원소를 넣게 된다면 그다음 stack_a의 상태도 정렬된 상태가 된다.
이 동작을 반복하면 모든 원소가 정렬된 상태로 stack_a에 들어가게 된다.
예시 1
먼저 선택을 반복하여 해답(stack_a에 모든 원소가 정렬된 상태)에 도달할 수 있는지 예시를 통해 살펴보자.
stack_a: 1 2 4 7 8
stack_b: 5 3 6 9
이 상태에서 5라는 원소를 stack_a에 넣고싶다면
ra ra ra를 통해 stack_a의 올바를 위치에 push 할 수 있도록 stack_a를 돌려주고
step1
stack_a: 7 8 1 2 4
stack_b: 5 3 6 9
pa
step2
stack_a: 5 7 8 1 2 4
stack_b: 3 6 9
rra rra rra를 통해 stack_a를 되돌려 주면
step3
stack_a: 1 2 4 5 7 8
stack_b: 3 6 9
짜잔~ 정렬되어 있는 stack_a에 5가 들어갔다.
위 예시에서 step1(돌리기), step2(넣기)를 stack_b의 원소 개수만큼 반복하고 마지막으로 step3을 수행하면 stack_b의 모든 원소를 stack_a에 정렬된 상태로 넣을 수 있다.
선택을 반복하여 해답에 도달하기
예시 1.1
예시1 이후 step1, step2를 반복
stack_a
- 5 7 8 1 2 4 (step1, step2)
- 3 4 5 7 8 1 2 (step1, step2)
- 6 7 8 1 2 3 4 5 (step1, step2)
- 9 1 2 3 4 5 6 7 8 (step1, step2)
- 1 2 3 4 5 6 7 8 9 (step3)
이렇게 step1, step2를 반복하고 마지막으로 step3을 실행하면 stack_b에 있던 원소들을 stack_a에 정렬된 상태로 넣을 수 있다는 것을 알 수 있었다.
하지만 이 방법이 각 단계에서 최선의 선택일까?
방금 보여준 예시는 push 하는 원소도 최선의 선택이 아니었고 push 하기 위해 stack_a를 돌린 것도 최선의 선택이 아니었다.
최선의 선택은 무엇일까?
예시 2
rrb pa ra
stack_a: 1 2 4 7 8
stack_b: 5 3 6 9
step1
stack_a: 1 2 4 7 8
stack_b: 9 5 3 6
step2
stack_a: 9 1 2 4 7 8
stack_b: 5 3 6
step3
stack_a: 1 2 4 7 8 9
stack_b: 5 3 6
원소 하나를 stack_a에서 stack_b로 옮기는 데 예시1에서 사용했던 명령의 절반도 사용하지 않았다. (7개 -> 3개)
최선의 선택을 하여 원소 하나를 이동시킨 것이다.
각 상황에서 최선의 선택 고르기
위에서 보인 예시 이외에도 최적의 선택을 하기 위해 여러 조건들을 고려해봐야 한다.
stack_b에서 stack_a로 push 하기 위해 각 스택을 돌리는 경우는 다음과 같다. (step1 수행)
(편의를 위해 stack의 top를 위쪽이라고 하겠다.)
- ra, rb를 사용해 stack_a, stack_b를 위쪽으로 돌리기
- ra, rrb를 사용해 stack_a를 위쪽, stack_b를 아래쪽으로 돌리기
- rra, rb를 사용해 stack_a를 아래쪽, stack_b를 위쪽으로 돌리기
- rra, rrb를 사용해 stack_a, stack_b를 아래쪽으로 돌리기
조금 더 최적화를 해보자면,
1의 경우, rr을 사용해 두 스택을 동시에 돌리고 남은 ra 또는 rb를 수행하기
4의 경우, rrr을 사용해 두 스택을 동시에 돌리고 남은 rra 또는 rrb를 수행하기
로 바꿀 수 있다.
최선의 선택을 위해 1, 2, 3, 4를 수행하기 위해 필요한 명령어의 개수를 각각 계산하고 명령어가 가장 적게 필요한 동작을 수행한다.
push_swap 구현
내가 구현한 프로그램은 크게 3단계로 구분되어 있다.
- 인자 처리 (예외처리 및 스택 초기화)
- stack_a -> stack_b 원소 이동
- stack_b -> stack_a 그리디 정렬
1. 인자처리
프로그램이 받은 인자에 대해 예외처리를 하고 stack_a를 초기화한다.

ps_check_arg()
main 함수 인자가 int 형인지 판단하고 중복 검사를 한다.
인자들이 모두 정상적이라면 argv를 int형으로 변환해 int_arr을 초기화한다.
ps_init()

int_arr로 stack_a를 초기화하는 함수이다.
stack_a에 원소를 넣을 때 자신보다 작은 원소의 개수만큼 content++ 하고 노드를 생성한다.
만약 "100 500 200 300 400"이 인자로 들어온다면 "0 4 1 2 3"으로 숫자가 바뀌어 stack_a에 들어가게 된다.
2. stack_a -> stack_b 원소 이동
단순히 stack_a를 stack_b로 옮기기만 하면 되는 거 아니야?라고 생각할 수 있지만
그리디 알고리즘을 사용할 때 명령어 개수를 줄이기 위한 최적화 작업이 포함되어 있다.
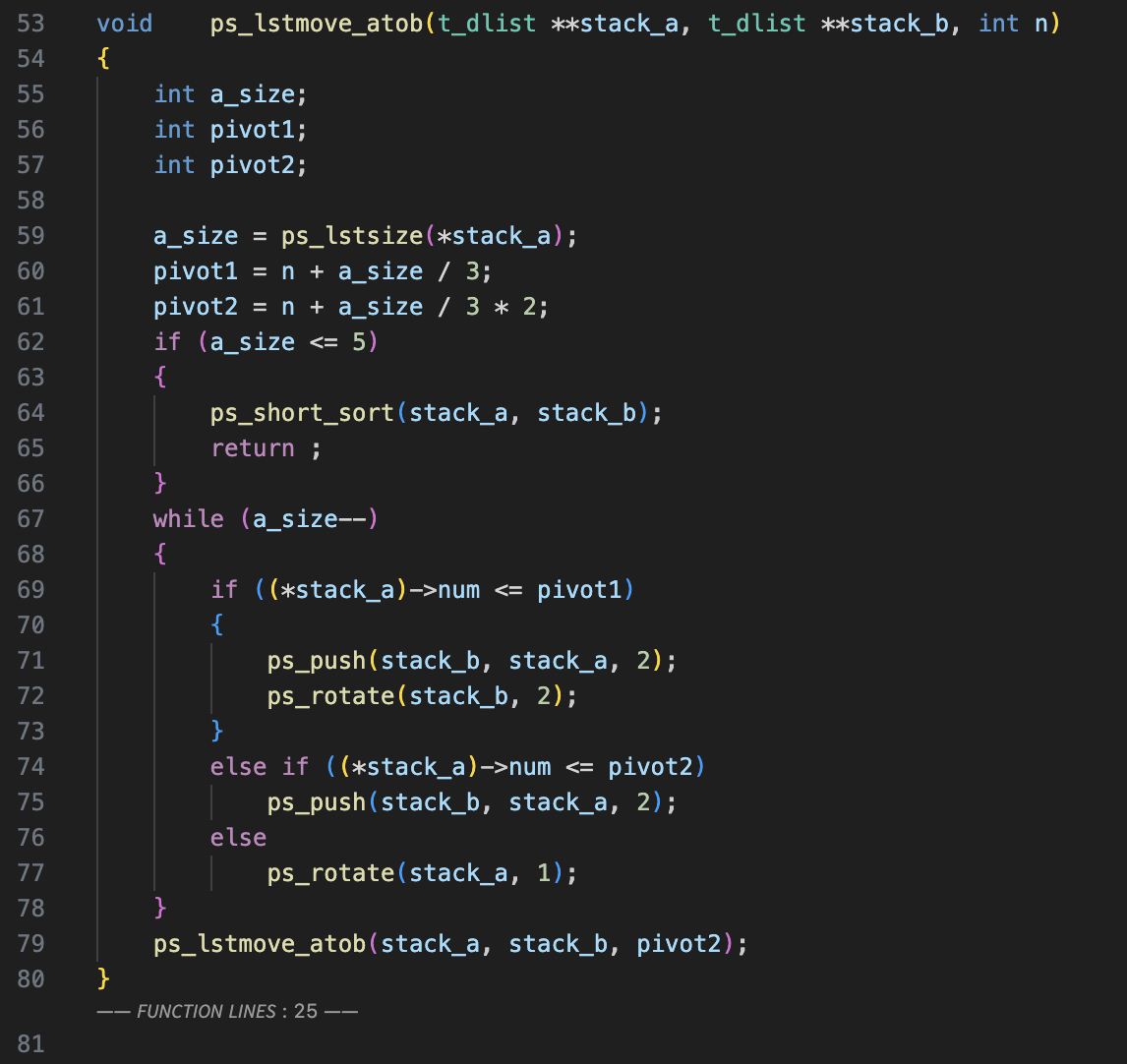
ps_lstmove_atob()
- stack_a에 원소가 5개 이하로 남을 때까지 함수를 재귀적으로 호출한다.
- stack_a의 원소를 3 등분하여 큰 값은 stack_b의 위쪽, 중간 값은 stack_b의 아래쪽, 작은 값은 stack_a의 아래쪽으로 이동시킨다.
- 해당 함수를 반복하면 stack_a에는 값이 가장 큰 정렬된 5개 이하의 원소가 존재하게 되고,
- stack_b에는 top, bottom으로 갈수록 값이 크고 middle으로 갈 수록 값이 작은 모래시계 형태로 원소들이 위치하게 된다.
이 함수를 통하여 최적화를 한다면, 이후에 그리디 알고리즘을 수행하며 stack_b의 위 또는 아래에서 원소를 반복적으로 빼낼 때
이전에 빼낸 원소와 비슷한 원소들이 원소를 빼낸 근처에 위치하게 되어 명령어 개수를 줄일 수 있다.
(push_swap의 특성상 스택의 위, 아래에 비슷한 원소들이 있을 때 rb, rrb를 사용해 접근하기 쉬워진다.)
3. stack_b -> stack_a 그리디 정렬

while 문이 포스팅 위쪽에서 설명했던 step1(돌리기), step2(push) 부분이고, if-else 문이 step3(최종 정렬) 부분이다.
while 문
포스팅 위쪽에서 push_swap 그리디 알고리즘을 설명할 때 말했듯이 stack_b에서 stack_a로 push 하기 위해 step1을 수행하는 방법 중 최선의 방법은 1, 2, 3, 4 중에 하나이다.
- A_H_B_H: 둘 다 위쪽으로 돌리기
- A_H_B_L: stack_a 위쪽, stack_b 아래쪽으로 돌리기
- A_L_B_H: stack_a 아래쪽, stack_b 위쪽으로 돌리기
- A_L_B_L: 둘 다 아래쪽으로 돌리기
해당 동작 중 어떤 동작을 수행할지는 ps_check_best() 함수가 결정한다.
ps_check_best()

요약하면, stack_b에서 stack_a에 원소를 넣기 위한 최선의 action을 선택하기 위한 함수이다.
stack_b의 모든 원소에 대해 각 원소의 b_pos에 대응하는 a_pos를 구하고 해당 position에 대한 명령어 개수의 최솟값을 구한다.
position에 대한 명령어의 개수가 step1을 수행하기 위한 최소값이라면 check_best 배열을 갱신한다.
check_best 배열에는 step1을 위한 최소 명령어 개수의 a_pos, b_pos, count_func, action이 저장된다.
- a_pos: stack_a에서 원소의 위치 - check_best[2]
- b_pos: stack_b에서 원소의 위치 - check_best[3]
- count_func: b_pos의 원소를 a_pos에 push 하기 전 step1을 수행하기 위한 최소 명령어 개수 - check_best[0]
- action: step1을 수행하기 위한 동작 - check_best[1]
- action은 A_H_B_H, A_H_B_L 등이다.
if-else 문
stack_a에 모든 원소가 들어갔으니 최종으로 stack_a를 정렬한다.
stack_a를 위 또는 아래로 돌려서 명령어가 적게 필요한 정렬을 수행한다.
예시) "2 3 4 5 1"이라면 rra를 수행하고, "4 5 1 2 3"이라면 ra ra를 수행한다.
후기
평가를 다니며 push_swap이 2서클 킬러 과제라는 소문을 많이 들어서 긴장을 하고 과제를 시작했는 데 그리디 알고리즘이 직관적이기도 하고 생각하는 대로 구현하면 구현도 크게 어렵지 않아서 과제를 하는 데 시간이 생각보다 적게 들었던 것 같다. 처음 push_swap를 접하면 막막한 감이 없잖아 있는데 그리디라는 직관적이고 매력적인 알고리즘을 떠올리고 구현해 볼 수 있어서 좋았다.
인터넷에 push_swap 그리디 알고리즘에 대한 글이 다른 알고리즘에 비해 상대적으로 적던데 클러스터 내에서 그리디 알고리즘이 어렵다는 얘기가 돌아 시도하는 사람이 적어서 그렇다고 생각한다. 하지만 직접 구현해보니 크게 어렵지는 않았어서 다른 분들도 그리디 알고리즘을 어렵게만 생각하지 말고 한번 시도해 보는 것도 좋을 것 같다고 생각한다.
push_swap Tester
과제 도중 참고했던 tester이다.
https://github.com/gemartin99/Push-Swap-Tester
GitHub - gemartin99/Push-Swap-Tester: Push_swap tester and bonus tester + GUI pro checker
Push_swap tester and bonus tester + GUI pro checker - gemartin99/Push-Swap-Tester
github.com
https://github.com/LeoFu9487/push_swap_tester
GitHub - LeoFu9487/push_swap_tester: This is a tester for school 42 project push_swap, made by yfu from 42LYON.
This is a tester for school 42 project push_swap, made by yfu from 42LYON. - LeoFu9487/push_swap_tester
github.com
'대외활동 > 42서울' 카테고리의 다른 글
| [42서울] ft_printf 구현 (한 문장으로 구현하는 이진수 보수 연산) (0) | 2024.06.21 |
|---|---|
| [42서울] Libft 함수 정리와 후기 (0) | 2024.03.20 |
| [42서울] Born2beroot 개념 정리 2 (0) | 2024.03.04 |
| [42서울] Born2beroot 개념 정리 1 (1) | 2024.03.04 |
| [42서울] 2023-2 라피신 후기 (0) | 2023.08.16 |