우선순위 큐
- 우선순위가 가장 높은(낮은) 원소르 먼저 삭제
- 임의의 우선순위를 가진 원소 삽입 가능
- 최대 우선순위 큐
template <class T>
class MaxPQ
{
public:
virtual ~MaxPQ() {}
// 가상 소멸자
virtual bool IsEmpty() const = 0;
// 우선순위 큐가 공백이면 true를 반환
virtual const T &Top() const = 0;
// 최대 원소에 대한 참조를 반환
virtual void Push(const T &) = 0;
// 우선순위 큐에 원소를 삽입
virtual void Pop() = 0;
// 최대 우선순위를 가진 원소를 삭제
};
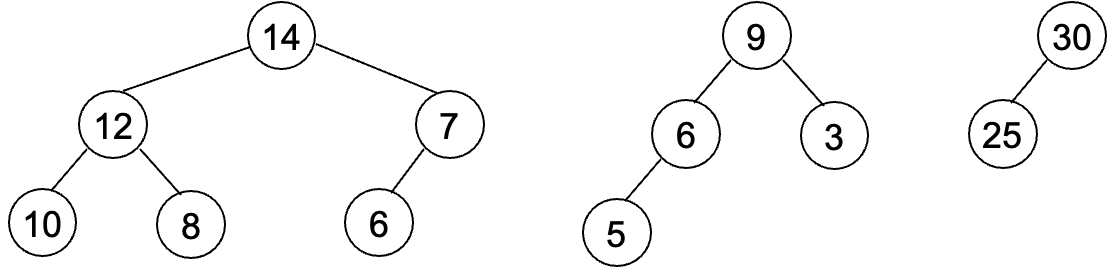
표현 방법 - 최대 히프
최대 히프
- 최대(최소) 트리: 각 노드의 키 값이 그 자식의 키 값보다 작지(크기) 않은 트리
- 최대 히프: 최대 트리이면서 완전 이진 트리
- 최소 히프: 최소 트리이면서 완전 이진 트리
template <typename T>
class MaxHeap : public MaxPQ
{
private:
T *heap; // 원소 배열
int heapSize; // 힙의 원소 개수
int capacity; // 힙 크기
public:
MaxHeap(int);
void Push(const T &);
void Pop();
// 그 외 함수들
//
};
최대 히프에서의 삽입
- 새로 삽입되는 원소는 부모 원소와 비교하면서 최대 히프가 되는 것이 확인될 때까지 위로 올라감

template <class T>
void MaxHeap<T>::Push(const T &e)
{ // 최대 힙에 e 삽입
if (heapSize == capacity)
{ // 크기를 2배로 확장
ChangeSize1D(heap, capacity, 2 * capacity);
capacity *= 2;
}
int currentNode = ++heapSize;
while (currentNode != 1 && heap[currentNode / 2] < e)
{
heap[currentNode] = heap[currentNode / 2]; // 부모 원소를 아래로 내림
currentNode /= 2; // 부모 원소로 이동
}
heap[currentNode] = e;
}
시간복잡도 - O(log n)
최대 히프에서의 삭제
- 루트에서 삭제
- 마지막 원소를 제거하고 제거된 마지막 원소와 루트의 왼쪽 자식, 오른쪽 자식 중 큰 값과 서로 교환
- 최대 히프가 될 때까지 원소 값을 비교하여 교환

template <class T>
void MaxHeap<T>::Pop()
{
if (IsEmpty())
throw "Heap is empty. Cannot delete.";
heap[1].~T(); // 가장 큰 원소 삭제
// lastE는 힙의 마지막 원소
T lastE = heap[heapSize--];
// trickle down
int currentNode = 1; // 루트 노드에서 작업 시작
int child = 2; // currentNode의 자식
while (child <= heapSize)
{
// currentNode 더 큰 자식을 위치
if (child < heapSize && heap[child] < heap[child + 1])
child++;
// currentNode 위치에 lastE가 존재해도 된다면
if (lastE >= heap[child])
break; // 작업 종료
heap[currentNode] = heap[child]; // 자식을 부모의 위치로 이동
currentNode = child; // 작업 위치 이동
child *= 2; // 작업 위치 이동
}
heap[currentNode] = lastE;
}
시간복잡도 - O(log n)
이진 탐색 트리
사전(dictionary)
- pair<키, 원소>의 집합
template <class K, class E>
class Dictionary
{
public:
virtual bool IsEmpty() const = 0;
// 공백이면 true 리턴
virtual pair<K, E> *Get(const K &) const = 0;
// 지시한 키를 가진 쌍에 대한 포인터 반환, 쌍이 없으면 0 반환
virtual void Insert(const pair<K, E> &) = 0;
// 쌍을 삽입, 키가 중복되면 관련 원소 갱신
virtual void Delete(const K &) = 0;
// 지시된 키를 가진 쌍 삭제
};
정의
- 이진트리로서 공백 가능하고, 만약 공백이 아니라면
- 모든 원소는 상이한 키를 갖음
- 왼쪽 서브트리의 키들은 그 루트의 키보다 작음
- 오른쪽 서브트리의 키들은 그 루트의 키보다 큼
- 왼쪽과 오른쪽 서브트리도 이원 탐색 트리

이진 탐색 트리의 탐색
k = 루트의 키: 성공적 종료
k < 루트의 키: 왼쪽 서브트리 탐색
k > 루트의 키: 오른쪽 서브트리 탐색
template <class K, class E> // Driver
pair<K, E> *BST<K, E>::Get(const K &k)
{ // 키 k를 가진 쌍을 이원 탐색 트리(*this)에서 탐색
// 쌍을 발견하면 포인터 반환, 아니면 0 반환
return Get(root, k);
}
template <class K, class E> // Workhorse
pair<K, E> *BST<K, E>::Get(TreeNode<pair<K, E>> *p, const K &k)
{
if (!p)
return 0;
if (k < p->data.first)
return Get(p->leftChild, k);
if (k > p->data.first)
return Get(p->rightChild, k);
return &p->data; // 데이터의 주소 값 반환
}
template <class K, class E> // 반복문 버전
pair<K, E> *BST<K, E>::Get(const K &k)
{
TreeNode<pair<K, E>> *currentNode = root;
while (currentNode)
if (k < currentNode->data.first)
currentNode = currentNode->leftChild;
else if (k > currentNode->data.first)
currentNode = currentNode->rightChild;
else
return ¤tNode->data;
// 매치하는 쌍 없음
return 0;
}
순위에 의한 이진 탐색 트리의 탐색
순위(rank)
- 중위 순서에서의 위치
- leftSize = 왼쪽 서브 트리의 원소 수 + 1

template <class K, class E> // 순위에 의한 탐색
pair<K, ~E> *BST<K, ~E>::RankGet(int r)
{ // r번째 작은 쌍을 탐색
TreeNode<pair<K, E>> *currentNode = root;
while (currentNode)
if (r < currentNode->leftSize)
currentNode = currentNode->leftChild;
else if (r > currentNode->leftSize)
{
r -= currentNode->leftSize;
currentNode = currentNode->rightChild;
}
else
return ¤tNode->data;
return 0;
}
이진 탐색 트리에서의 삽입
- x의 key값을 가진 노드를 탐색
- 탐색이 성공하면 이 키에 연관된 원소를 변경
- 탐색이 실패하면 탐색이 끝난 지점에 쌍을 삽입

template <class K, class E>
void BST<K, E>::Insert(const pair<K, E> &thePair)
{ // 이진 탐색 트리에 pair 삽입
// thePair.first를 탐색, pp는 p의 부모
TreeNode<pair<K, E>> *p = root, *pp = 0;
while (p)
{
pp = p;
if (thePair.first < p->data.first)
p = p->leftChild;
else if (thePair.first > p->data.first)
p = p->rightChild;
else // 복제, 연결된 요소 업데이트
{
p->data.second = thePair.second;
return;
}
}
// 노드를 생성
p = new TreeNode<pair<K, E>>(thePair);
if (root) // 공백 트리가 아닐 경우
if (thePair.first < pp->data.first)
pp->leftChild = p;
else
pp->rightChild = p;
else
root = p; // 공백 트리라면 생성한 노드를 루트에 위치시킴
}
이진 탐색 트리에서의 삭제
리프 원소의 삭제
- 부모의 자식 필드에 0을 삽입, 삭제된 노드 반환
하나의 자식을 가진 비리프 노드의 삭제
- 삭제된 노드의 자식을 삭제된 노드의 자리에 위치
두개의 자식을 가진 비리프 노드의 삭제
- 왼쪽 서브트리에서 가장 큰 원소나 오른쪽 서브트리에서 가장 작은 원소로 대체
- 대체된 서브트리에서 대체한 원소의 삭제 과정 진행
시간복잡도 - O(h)
이원 탐색 트리의 원소 수: n
최악의 경우
- 이원 탐색 트리의 높이 = n
삽입 삭제가 무작위로 이루어질 때
- 트리의 높이 = O(log n)
균형 탐색 트리
- 최악의 경우에도 높이가 O(log n)이 되는 트리
- 탐색, 삽입, 삭제의 시간 복잡도: O(h)
'전공 > 자료구조' 카테고리의 다른 글
| [자료구조] 그래프 2 (신장 트리, Kruskal, Prim, Sollin 알고리즘, 그래프 최단경로, AOV 네트워크) (0) | 2023.05.30 |
|---|---|
| [자료구조] 그래프 1 (그래프 정의, 그래프 표현, 그래프 탐색) (0) | 2023.05.30 |
| [자료구조] 트리 1 (트리 종류, 이진 트리 순회, 복사, 동일성 검사) (0) | 2023.05.12 |
| [자료구조] 연결 리스트 4 (연결 스택과 큐, 다항식, 이중 연결 리스트) (0) | 2023.05.12 |
| [자료구조] 연결 리스트 3 (원형 리스트, 가용 공간 리스트) (0) | 2023.05.12 |