728x90
반응형
그래프

정의
그래프 G: 2개의 집합 V, E로 구성
- V: 공집합이 아닌 정점(vertex)의 유한집합
- E: 간선(edges)이라고 하는 정점 쌍들의 집합
- 표기: G = (V, E)
그래프의 제약 사항
- 자기 간선 또는 자기 루프 없음
- 동일 간선의 중복 없음
| 무방향 그래프 | 간선을 나타내는 정점의 쌍에 순서 없음 (u, v) = (v, u) |
| 방향 그래프 | 방향을 가지는 정점의 쌍 <u, v>로 표시 <u, v> ≠ <u, v> |
| 완전 그래프 | n개의 정점과 n(n-1)/2개의 간선을 가진 그래프 |
| 그래프 G의 부분그래프(subgraph) | v(G') ⊆ V(G) 이고 E(G') ⊆ E(G)인 그래프 G' |
(u, v)가 E(G)의 한 간선이라면
- u와 v는 인접
- 간선 (u, v)는 정점 u와 v에 부속
정점 u로부터 정점 v까지의 경로
- 그래프 G에서 \((u, i_{1}), (i_{1}, i_{2}, ..., (i_{k}, v\)를 E(G)에 속한 간선이라 할 떼,
u로부터 v까지의 경로는 \(u, i_{1}, i_{2}, ..., i_{k}, v\)
경로의 길이(length)
- 경로상에 있는 간선의 수
- (0, 1), (1, 3), (3, 2) == 0, 1, 3, 2
- -> 길이가 3인 경로
단순 경로
- 경로상에서 처음과 마지막을 제외한 모든 정점들이 서로 다름
단순 방향 경로
- 같은 정점을 두번 이상 방문하지 않는 방향 그래프의 간선의 일련
사이클
- 처음과 마지막 정점이 같은 단순 경로
연결 요소
- 최대 연결 부분 그래프

강력 연결
- 방향 그래프에서 V(G)에 속한 서로 다른 두 정점 u, v의 모든 쌍에 대해서, u에서 v로, 또한 v에서 u로의 방향 경로가 존재
강력 연결 요소
- 강력 연결된 최대 부분 그래프
- 차수 - 정점에 부속한 간선들의 수
- 진입차수 - 임의의 정점 v가 머리가 되는 간선들의 수
- 진출차수 - v가 꼬리가 되는 간선들의 수
- 간선의 수 - \(e=\sum_{i=0}^{n-1}d_{i}/2\) (n개의 정점과 e개의 간선을 가진 그래프
- 다이그래프 - 방향 그래프
- 그래프 - 무방향 그래프
코드
class Graph
{
public:
virtual ~Graph() {}
// 가상 소멸자
bool IsEmpty() const {return n == 0};
// 그래프에 정점이 없으면 true
int NumberOfVertices() const {return n};
// 그래프의 정점 수 반환
int NumberOfEdges() const {return e};
// 그래프의 간선 수 반환
virtual int Degree(int u) const = 0;
// 정점 v에 인접한 간선의 수 반환
virtual bool ExistsEdge(int u, int v) const = 0;
// 그래프에 간선 (u,v)가 있으면 true
virtual void InsertVertex(int v) = 0;
// 정점 v를 삽입, v는 인접한 간선 없음
virtual void InsertEdge(int u, int v) = 0;
// 간선 (u, v)를 그래프에 삽입
virtual void DeleteVertex(int v) = 0;
// 정점 v와 이에 인접한 모든 간선 삭제
virtual void DeleteEdge(int u, int v) = 0;
// 그래프에 간선 (u, v)를 삭제
private:
int n; // 정점의 수
int e; // 간선의 수
};
그래프 표현법
인접행렬(Adjacency Matrix)
- 간선 (\(v_{i}, v_{j}\)) 존재: a[i][j] = 1
- 간선 (\(v_{i}, v_{j}\)) 존재x: a[i][j] = 0
- 필요 공간: \(n^{2}\)비트

- 무방향 그래프: 어떤 정점 i의 차수는 그 행의 합
- 방향 그래프: 행의 합은 진출차수, 열의 합은 진입차수
- 인접행렬의 수행 시간 - O(\(n^{2}\))
- 희소 그래프로 변경 - O(e+n)
인접리스트(AdjacencyLists)
- 인접 행렬의 n행들을 n개의 연결리스트로 표현
- data, link필드
- C++선언문
- Chain<int> *adjList; LinkedGraph(const int vertice = 0): n(vertices), e(0) { adhjist = new Chain<int>[n]; }
- n개의 정점, e개 간선의 무방향 그래프 - 크기가 n인 배열, 2e개의 체인 노드 필요
- 방향 그래프: e개의 체인 노드

가중치 간선(Weighted Edges)
- 그래프의 간선에 가중치 부여
- 인접행렬: 행렬 엔트리에 a[i][j]의 가중치 정보 저장
- 인접리스트: 노드 구조에 weight 필드 추가
- 네트워크: 가중치 간선을 가진 그래프
그래프 탐색
깊이 우선 탐색
virtual void Graph::DFS()
{
visited = new bool[n];
// 방문 여부 저장
fill(visited, visited + n, false);
DFS(0); // 정점 0에서 검색 시작
delete[] visited;
}
virtual void Graph::DFS(const int v)
{ // 방문 가능하며 방문하지 않았던 모든 정점 방문
visited[v] = true;
for (each vertex w adjacent to v) // 실제 코드는 반복자 사용
if (!visited[w])
DFS(w);
}
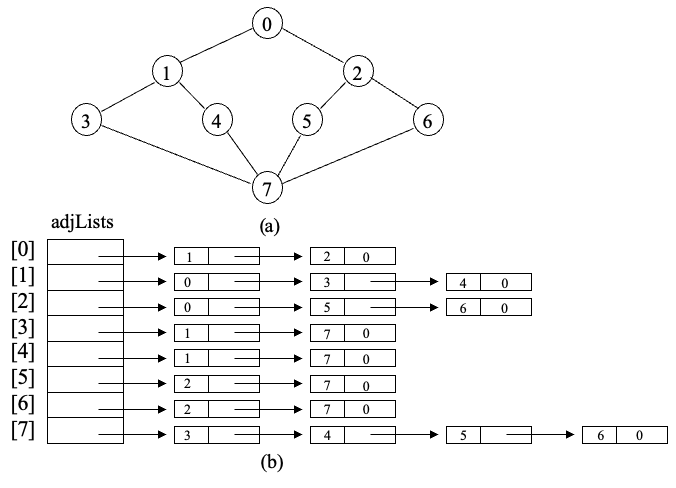
시간복잡도(인접 리스트) - O(e+n)
시간복잡도(인접 행렬) - O(\(n^{2}\))
너비 우선 탐색
virtual void Graph::BFS(int v)
{ // 정점 v에서 부터 시작
// v 방문시 visited[i]는 true로 설정, 큐 이용
// 그래프 (a)의 경우 0, 1, ..., 7 순서로 방문
visited = new bool[n];
fill(visited, visited + n, false);
visited[v] = true;
Queue<int> q;
q.Push(v);
while (!q.IsEmpty())
{
v = q.Front();
q.Pop();
for (all vertices w adjacent to v) // 실제 코드는 반복자 사용
if (!visited[w])
{
q.Push(w);
visited[w] = true;
}
}
delete[] visited;
}
시간복잡도(인접 리스트) - O(e+n)
시간복잡도(인접 행렬) - O(\(n^{2}\))
연결 요소
방문하지 않은 정점 v에 대해 DFS(v) 또는 BFS(v)를 반복 호출로 구함
virtual void Graph::Components()
{ // 그래프의 연결 요소들을 결정
visited = new bool[n];
fill(visited, visited + n, false);
for (i = 0; i < n; i++)
if (!visited[i])
{
DFS(i); // 연결 요소를 탐색
OutputNewComponent();
}
delete[] visited;
}
시간복잡도(인접 리스트) - O(n+e)
시간복잡도(인접 행렬) - O(\(n^{2}\))
728x90
반응형
'전공 > 자료구조' 카테고리의 다른 글
| [자료구조] 탐색 (순차 탐색, 이원 탐색, 두 리스트 비교) (1) | 2023.05.30 |
|---|---|
| [자료구조] 그래프 2 (신장 트리, Kruskal, Prim, Sollin 알고리즘, 그래프 최단경로, AOV 네트워크) (0) | 2023.05.30 |
| [자료구조] 트리 2 (최대 히프, 이진 탐색 트리) (2) | 2023.05.19 |
| [자료구조] 트리 1 (트리 종류, 이진 트리 순회, 복사, 동일성 검사) (0) | 2023.05.12 |
| [자료구조] 연결 리스트 4 (연결 스택과 큐, 다항식, 이중 연결 리스트) (0) | 2023.05.12 |