728x90
반응형
정렬
리스트를 오름차순, 내림차순 혹은 어떤 조건에 대해 순서대로 배열한 것
정렬에 필요성
- 빠른 탐색을 위해 사용
- 리스트의 엔트리를 비교하는 방법으로 사용
정렬 방법
- 내부 방법 - 정렬할 리스트가 작아서 전체적인 정렬이 메인 메모리 상에서 실행될 수 있을 때 사용
- 외부 방법 - 큰 리스트에 사용
삽입 정렬
template <class T>
void Insert(const T &e, T *a, int i)
{ // e를 정렬된 리스트 a[1:i]에 삽입
// 리스트 a[1:i+1]도 정렬되게 함
// 배열 a는 적어도 i+2 원소를 포함할 공간 필요
a[0] = e;
while (e < a[i])
{ // 리스트의 맨 뒤부터 e가 삽입될 위치인지 탐색하며,
a[i + 1] = a[i]; // 배열 a의 원소를 한칸씩 위로 이동
i--;
}
a[i + 1] = e;
}
template <class T>
void InsertionSort(T *a, const int n)
{ // 삽입 정렬
for (int j = 2; j <= n; j++)
{ // 기존 리스트의 앞부터 순차로 원소를 배열
T temp = a[j];
Insert(temp, a, j - 1);
}
}
시간복잡도 - O(\(n^{2}\))
삽입 정렬의 변형
이원 삽입 정렬
- Insert에서 사용된 순차 탐색 기법 대신 이원 탐색을 사용
- 삽입 정렬에서 수행하는 비교 횟수 감소
- 레코드 이동 횟수는 그대로
연결 삽입 정렬
- 리스트의 원소들을 배열 대신 연결 리스트로 표현
- 링크 필드만 조정하면 됨, 이동 횟수 0
퀵 정렬

- 정렬할 레코드 중 pivot 레코드를 선택
- 정렬한 레코드들을 다시 정돈
- pivot의 왼쪽: pivot의 키보다 작거나 같은 레코드들을 위치 시킴
- pivot의 오른쪽: pivot의 키보다 크거나 같은 레코드들을 위치 시킴
- 퀵 정렬을 순환적으로 사용
- pivot의 왼쪽과 오른쪽 레코드들은 서로 독립적으로 정렬
코드
template <class T>
void QuickSort(T *a, const int left, const int right)
{ // 배열 a[left:right]를 비감소 순으로 정렬
// a[left]는 피봇으로 사용
// 왼쪽에서 비봇보다 큰 수, 오른쪽에서 피봇보다 작은 수를 찾아 위치 교환
if (left < right)
{
int i = left,
j = right + 1,
pivot = a[left];
do
{
do i++; while (a[i] < pivot);
do j--; while (a[j] > pivot);
if (i < j) swap(a[i], a[j]);
} while (i < j);
swap(a[left], a[j]);
QuickSort(a, left, j - 1);
QuickSort(a, j + 1, right);
}
}
시간복잡도 - O(\(n^{2}\))
평균 연산 시간 - O(n log n)
퀵 정렬은 순환을 구현하기 위해 스택 공간 필요
리스트가 균등하게 나뉘는 경우 - O(log n)
최악의 경우 - O(n)
합병 정렬
합병(Merging)
두개의 정렬된 리스트를 하나의 정렬된 리스트로 합병

입력 리스트가 1인 n개의 정렬된 서브리스트로 간주
- 리스트들을 쌍으로 합병하여 크기가 2인 n/2개의 리스트 얻음
- n/2개의 리스트를 다시 쌍으로 합병하여 n/4개의 리스트 얻음
- 합병 단계는 하나의 서브리스트가 남을 때까지 계속됨
코드
template <class T>
void Merge(T *initList, T *mergedList, const int l, const int m, const int n)
{ // initList[l:m]과 initList[m+1:n]는 정렬된 리스트
// 이들을 정렬된 리스트 mergedList[l:n]으로 합병
int i1 = l, iResult = l, i2 = m + 1 // i1, i2와 iResult는 리스트 위치
for (; i1 <= m && i2 <= n; // 어떤 입력 리스트도 소진되지 않음
iResult++)
if (initList[i1] <= initList[i2])
{
mergedList[iResult] = initList[i1];
i1++;
}
else
{
mergedList[iResult] = initList[i2];
i2++;
}
// 첫번째 리스트의 나머지 레코드(남았다면) 복사
copy(initList + i1, initList + m + 1, mergedList + iResult);
// 두번째 리스트의 나머지 레코드(남았다면) 복사
copy(initList + i2, initList + n + 1, mergedList + iResult);
}
template <class T>
void MergePass(T *initList, T *resultList, const int n, const int s)
{ // 크기가 s인 서브리스트의 인접 쌍들이 initList에서 resultList로 합병, n은 initList의 레코드 수
int i = 1; // i는 합병되는 리스트의 첫 번째 위치
for (; i <= n - 2 * s + 1; // 길이가 s인 두 서브리스트를 위해 원소들이 충분한지?
i += 2 * s)
Merge(initList, resultList, i, i + s - 1, i + 2 * s - 1);
// 2*s보다 작은 나머지 리스트 합병
if ((i + s - 1) < n)
Merge(initList, resultList, i, i + s - 1, n);
else
copy(initList + i, initList + n + 1, resultList + i);
}
template <class T>
void MergeSort(T *a, const int n)
{ // [1:n]을 비감소 순으로 정렬
T *tempList = new T[n + 1];
// l은 현재 합병 중인 하위 목록의 길이
for (int l = 1; l < n; l *= 2)
{
MergePass(a, tempList, n, l);
l *= 2;
MergePass(tempList, a, n, l); // a와 tempList 역할 교환
}
delete[] tempList;
}
시간복잡도 - O(n log n)
합병 정렬의 문제점
정렬한 레코드 수에 비례해 저장 공간이 추가로 필요
힙 정렬
일정한 양의 저장 공간만 추가로 필요
왼쪽 및 오른쪽 서브트리가 모두 히프인 이진트리에서 시작하여 이진트리 전체가 최대 히프가 되도록 재조정


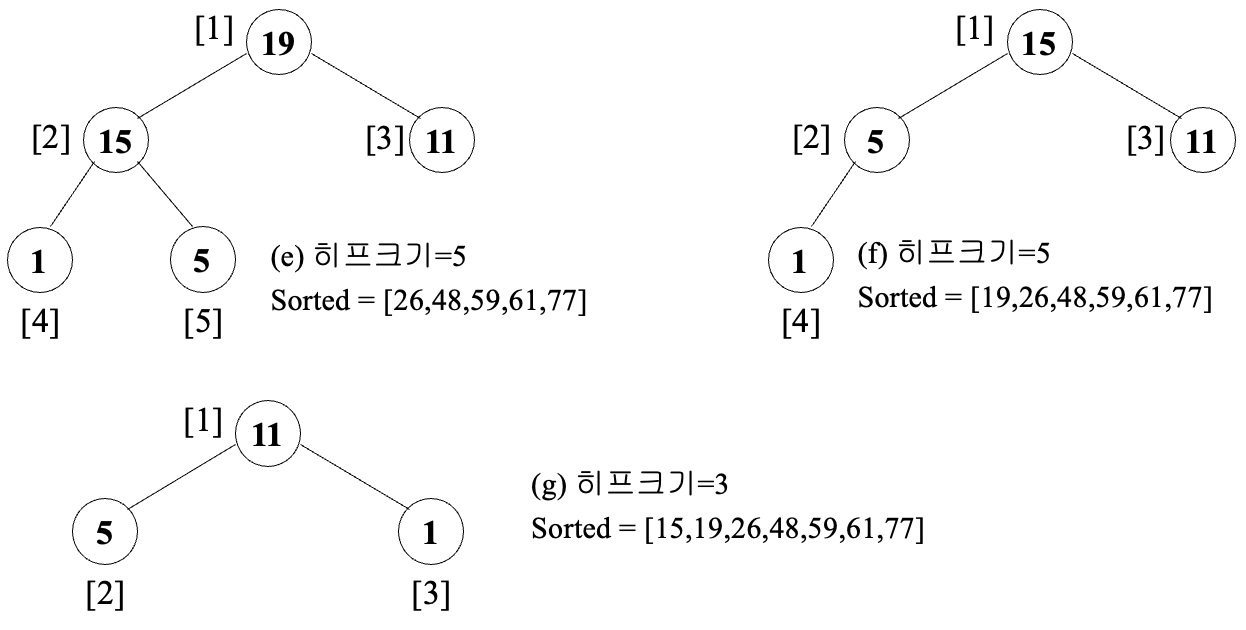
- Adjust를 반복적으로 호출 -> 최대 히프 구조를 만듬
- 히프의 첫 번째 레코드와 마지막 레코드를 교환
최대 키를 가진 레코드가 정렬된 배열의 정확한 위치에 자리 잡게 됨 - 히프의 크기를 줄인 후 히프를 재조정
코드
template <class T>
void Adjust(T *a, const int root, const int n)
{ // 루트 root를 가진 이진트리를 히프 성질을 만족하도록 조정
// root의 왼쪽과 오른쪽 서브트리는 히프 성질을 이미 만족
T e = a[root];
// e에 대학 적절한 위치를 탐색
for (int j = 2 * root; j <= n; j *= 2)
{
if (j < n && a[j] < a[j + 1])
j++; // j는 부모의 최대 자식
if (e >= a[j])
break; // e는 j의 부모로 삽입
a[j / 2] = a[j]; // j번째 레코드를 트리 위로 이동
}
a[j / 2] = e;
}
template <class T>
void HeapSort(T *a, const int n)
{ // a[1:n]을 비감소 순으로 정렬
for (int i = n / 2; i >= 1; i--) // 히프로 조정
Adjust(a, i, n);
for (i = n - 1; i >= 1; i--) // 정렬
{
swap(a[1], a[i + 1]); // 현 히프의 처음과 마지막을 교환
Adjust(a, 1, i); // 히프로 조정
}
}
시간복잡도 - O(n lon n)
기수 정렬
어떤 기수 r을 이용하여 정렬 키를 몇 개의 숫자로 분해
- r = 10: 키를 십진수로 분할
- r = 2: 키를 이진수로 분할
기수-r 정렬에서는 r개의 빈이 필요
각 빈의 레코드는 빈의 첫 레코드를 가리키는 포인터와 마지막 레코드를 가리키는 포인터를 통해 체인으로 연결
체인은 큐처럼 동작
기수 정렬 예시
범위가 [0, 999]인 십진수를 정렬 (d = 3, r = 10)



시간복잡도 - O(d(n+r))
d - 패스를 처리하면서 각 패스의 연산 시간은 O(n+r)
내부 정렬 비교
- 삽입 정렬 - 리스트가 부분적으로 정렬되어 있을 때 좋음, n이 작을 때 가장 좋음
- 합병 정렬 - 최악의 경우에 가장 좋음, 힙 정렬에 비해 많은 공산 사용
- 퀵 정렬 - 평균 성능이 가장 좋음, 최악의 경우 O(\(n^{2}\))
| 방법 | 최악의 경우 | 평균의 경우 |
| 삽입 정렬 | \(n^{2}\) | \(n^{2}\) |
| 힙 정렬 | \(n log n\) | \(n log n\) |
| 합병 정렬 | \(n log n\) | \(n log n\) |
| 퀵 경렬 | \(n^{2}\) | \(n log n\) |
728x90
반응형
'전공 > 자료구조' 카테고리의 다른 글
| [자료구조] 정렬 2 (외부 정렬 - 합병 정렬) (1) | 2023.06.06 |
|---|---|
| [자료구조] 탐색 (순차 탐색, 이원 탐색, 두 리스트 비교) (1) | 2023.05.30 |
| [자료구조] 그래프 2 (신장 트리, Kruskal, Prim, Sollin 알고리즘, 그래프 최단경로, AOV 네트워크) (0) | 2023.05.30 |
| [자료구조] 그래프 1 (그래프 정의, 그래프 표현, 그래프 탐색) (0) | 2023.05.30 |
| [자료구조] 트리 2 (최대 히프, 이진 탐색 트리) (2) | 2023.05.19 |